[2164] 카드2

import sys
input = sys.stdin.readline
from collections import deque
n = int(input())
card = deque()
for i in range(1, n+1):
card.append(i)
while len(card)>1:
# 제일 위에 있는 카드 바닥에 버리기
card.popleft()
# 제일 위에 있는 카드 제일 아래에 있는 카드 밑으로 옮기기
c = card.popleft()
card.append(c)
print(card[-1])
큐 자료구조를 이용해 문제를 풀었다.
자료구조를 이해하고 있다면 쉽게 풀 수 있는 문제다.
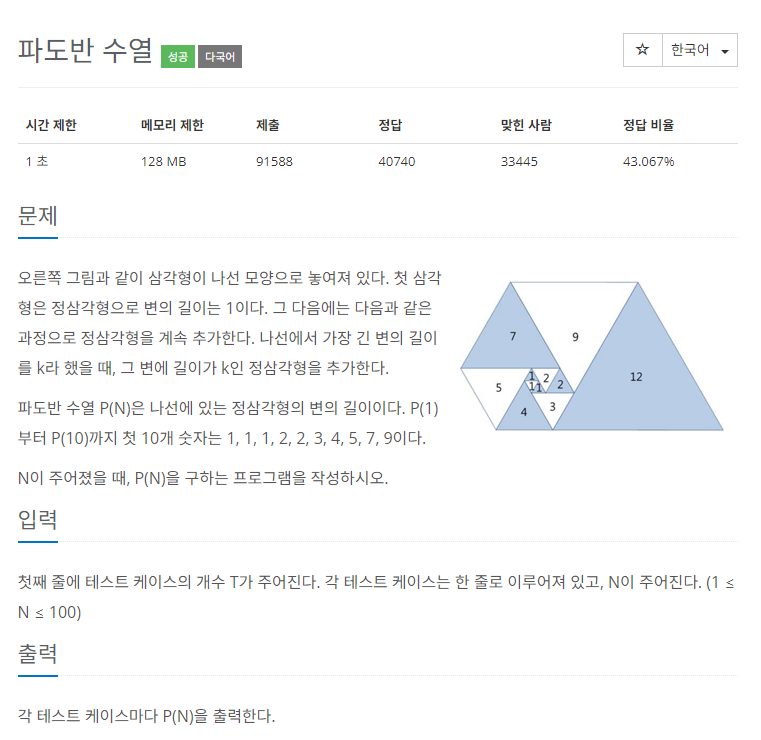
[9461] 파도반 수열
import sys
input = sys.stdin.readline
t = int(input())
for _ in range(t):
n = int(input())
p = [0]*101
p[1], p[2], p[3] = 1, 1, 1
p[4], p[5] = 2, 2
for i in range(6, n+1):
p[i] = p[i-5] + p[i-1]
print(p[n])DP 문제였다. 점화식을 찾기 위해서 p[1]부터 p[12]까지의 값을 적어놓고 규칙을 찾아보았다.
p[1]~p[5] 까지는 따로 규칙이 없고
p[6]부터 규칙이 생긴다.
p[6] = p[1] + p[5]
p[7] = p[2] + p[6]
p[8] = p[3] + p[7]
(중략)
p[n] = p[n-5] + p[n-1] 이라는 점화식을 알아낼 수 있게 됐다.
[11727] 2 * N 타일링 2
import sys
input = sys.stdin.readline
n = int(input())
d = [0]*1001
d[1] = 1
d[2] = 3
for i in range(3, n+1):
d[i] = 2*d[i-2] + d[i-1]
print(d[n]%10007)
이 문제도 DP 문제이다. 규칙을 찾기 위해 d[6]까지 값을 구해봤다.
d[1] = 1
d[2] = 3
d[3] = 5
d[4] = 11 = (3+5)+3
d[5] = 21 = (5+11)+5
d[6] = 43 = (11+21)+11
d[n] = d[n-2] + d[n-1] + d[n-2]
= 2*d[n-2] + d[n-1]
[2193] 이친수
import sys
input = sys.stdin.readline
n = int(input())
d = [0]*91
d[1], d[2] = 1, 1
for i in range(3, n+1):
d[i] = d[i-2] + d[i-1]
print(d[n])
DP 문제! d[n] = d[n-2] + d[n-1]의 점화식이 나온다.
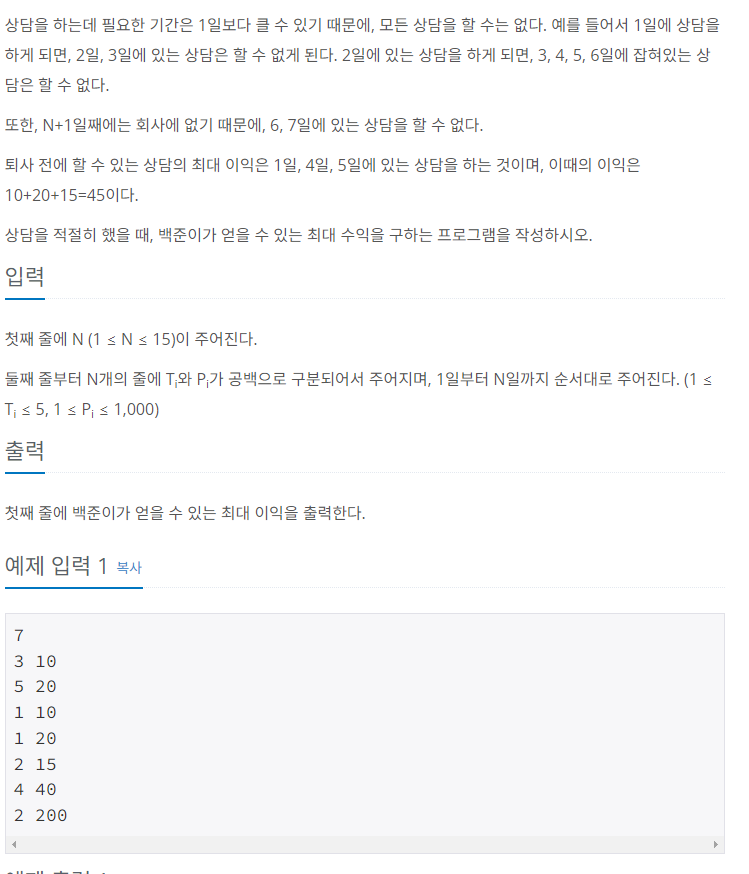
[14501] 퇴사

import sys
input = sys.stdin.readline
n = int(input())
T, P = [0], [0]
dp = [0]*(n+2) # 0 ~ n+1일(퇴사일까지)
for _ in range(n):
t, p = map(int, input().split())
T.append(t)
P.append(p)
for i in range(1, n+1):
for j in range(i+T[i], n+2): # j: 이후 상담 가능한 날짜
# i일에 시작한 상담의 종료일이 퇴사일, 퇴사일 이후인 경우 계산 X
if j>n+1:
continue
dp[j] = max(dp[j], dp[i]+P[i])
print(dp[n+1])

문제 이해가 되지 않는 사람들을 위해 하나하나 확인하며 설명해 보겠다.
실제로 DP 문제를 처음 접했을 때 다른 사람들의 글을 읽어도 전혀 이해가 안됐던 1인
1일에 상담을 진행하면 4일 이전까지는 상담을 진행할 수 없다.
즉, 4~7일에 새로운 상담 여부를 검토할 수 있다.
1일에 예약된 상담을 진행했을 때 DP는 [0, 0, 0, 0, 10, 10, 10, 10, 10]이 된다. (index는 0부터 8일까지!)
------------------------------------------------------------------------------------------------------------------------------------------------------------
2일에 상담을 진행하면 7일 이전까지는 상담을 진행할 수 없다.
즉, 7일에만 새로운 상담 여부를 검토할 수 있다.
2일에 예약된 상담을 진행했을 때 DP는 [0, 0, 0, 0, 10, 10, 10, 20, 20]이 된다.
2일에 상담을 진행하면 7일에 상담 금액 20원을 벌 수 있기 때문에
1일에 예약된 상담을 진행했을 때보다 더 많은 금액을 얻을 수 있다. 따라서 최댓값으로 업데이트 해준다.
------------------------------------------------------------------------------------------------------------------------------------------------------------
3일에 상담을 진행하면 4일 이전까지는 상담을 진행할 수 없다.
즉, 4~7일에 새로운 상담 여부를 검토할 수 있다.
3일에 예약된 상담을 진행했을 때 DP는 [0, 0, 0, 0, 10, 10, 10, 20, 20]이 된다.
3일에 상담을 진행하면 4일에는 상담 금액 10원을 벌 수 있기 때문에 따로 값이 업데이트 되지는 않는다.
------------------------------------------------------------------------------------------------------------------------------------------------------------
4일에 상담을 진행하면 5일 이전까지는 상담을 진행할 수 없다.
즉, 5~7일에 새로운 상담 여부를 검토할 수 있다.
4일에 예약된 상담을 진행했을 때 DP는 [0, 0, 0, 0, 10, 30, 30, 30, 30]이 된다.
왜냐하면 4일에 상담을 진행하면 5일에 상담 금액 20원을 받을 수 있기 때문에
4일까지 벌어놨던 최대 금액 10원에 20원이 더해지므로 5일부터는 30원을 최대로 벌 수 있게 된다.
------------------------------------------------------------------------------------------------------------------------------------------------------------
5일에 상담을 진행하면 7일 이전까지는 상담을 진행할 수 없다.
즉, 7일에만 새로운 상담 여부를 검토할 수 있다.
5일에 예약된 상담을 진행했을 때 DP는 [0, 0, 0, 0, 10, 30, 30, 45, 45]가 된다.
5일까지 벌어놨던 최대 금액 30원에 상담 금액인 15원을 상담 종료일인 7일에 받기 때문에
30원에 15원을 더한 45원으로 값이 업데이트 된다.
------------------------------------------------------------------------------------------------------------------------------------------------------------
6일에 상담을 진행하면 10일에 상담이 종료되므로, 이미 퇴사하고 없는 상태이다.
따라서 6일은 따로 상담을 진행하지 않고, 지금까지 번 최댓값 45원으로 만족해야 한다.
------------------------------------------------------------------------------------------------------------------------------------------------------------
7일에 상담을 진행하면 9일에 상담이 종료되므로, 이미 퇴사하고 없는 상태이다.
이 경우도 마찬가지로 따로 상담을 진행하지 않게 되고 for문이 끝난다.
최종적으로 dp[8]이 결괏값이 된다.
이는 퇴사일에 받을 수 있는 최댓값을 의미한다.
[11659] 구간 합 구하기4
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
nums = list(map(int, input().split()))
cumul = [0]
total = 0
for num in nums:
total += num
cumul.append(total)
for _ in range(m):
i,j = map(int, input().split())
print(cumul[j]-cumul[i]+nums[i-1])
슬라이싱해서 sum해주면 분명 시간 초과가 뜰 것 같아서 누적합을 이용했다.
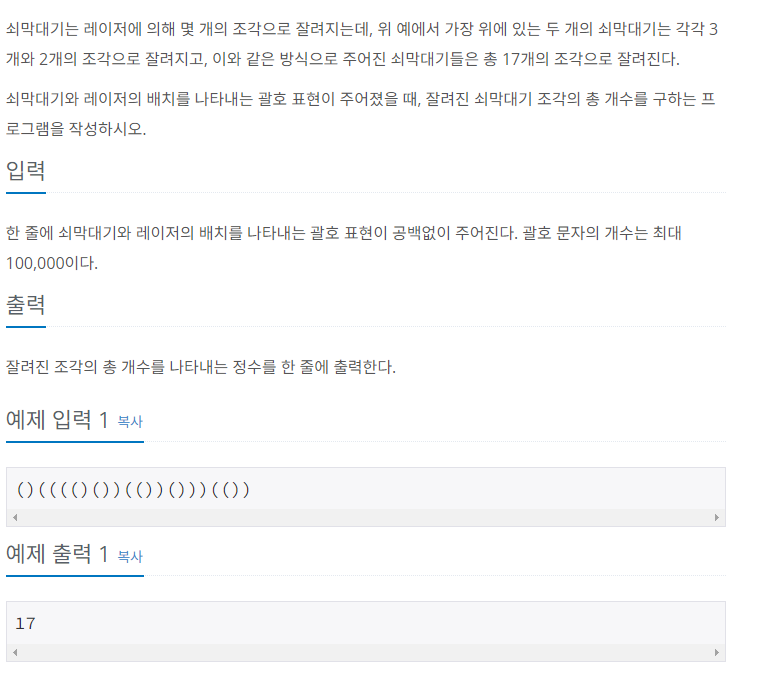
[10799] 쇠막대기

import sys
input = sys.stdin.readline
s = input().rstrip()
s = s.replace('()', '*')
s = list(s)
stick = 0
total = 0
while s:
p = s.pop()
if p==')': # 막대 시작
stick += 1
elif p=='*': # 현재 있는 막대 갯수만큼 잘려나옴
total += stick
else: # 막대 끝, 막대 갯수 -1, 마지막으로 잘려나온 갯수 +1
stick -= 1
total += 1
print(total)
연속으로 ()가 오는 경우에는 레이저로 취급하기 때문에 나는 따로 replace를 사용해서 *로 바꿔주었다.
입력받은 s를 오른쪽 끝부터 pop하면서 문자열을 비교하게 된다.
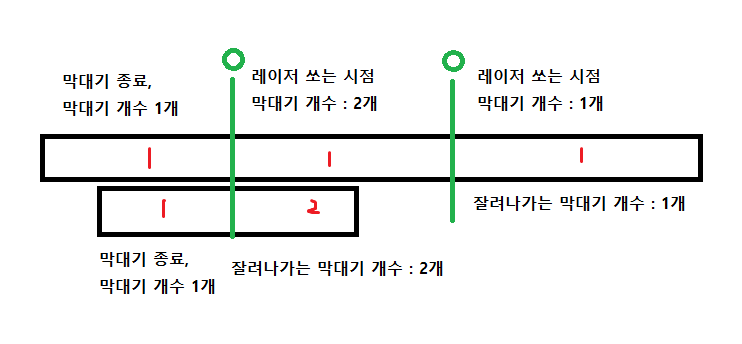
1. s.pop() == ' ) ' 인 경우 막대가 생기는 시점이다.
2. s.pop() == ' * ' 인 경우 레이저를 쏨으로써 현재까지 있던 막대기의 수만큼 잘려나온다.
3. s.pop() == ' ( ' 인 경우 막대기가 사라지는 시점이기 때문에 마지막으로 잘려나간 막대기가 1개 존재한다.
)를 만나면 막대 갯수를 1 증가시켜주고,
(를 만나면 막대 갯수를 1 감소시켜주면서, 잘려나간 막대기 개수도 total에 1 누적해준다.
레이저(*)를 만나면 지금까지 가지고 있는 막대기 개수만큼 total에 누적시킨다.
이 패턴만 이해되면 코드 작성하는 것은 간단하다!
'Algorithm' 카테고리의 다른 글
| 백준, 프로그래머스) 문제 풀이 (0) | 2023.09.30 |
|---|---|
| 백준 알고리즘) Silver 2 문제 랜덤 풀이 (0) | 2023.09.23 |
| 백준 알고리즘) 그래프 문제 풀이 (0) | 2023.09.17 |
| 백준 알고리즘) 정렬 문제 풀이 (1) | 2023.09.17 |
| 백트래킹 문제 풀이(Silver) (0) | 2023.09.16 |



